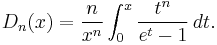Debye function
In mathematics, the family of Debye functions is defined by
The functions are named in honor of Peter Debye, who came across this function (with n = 3) in 1912 when he analytically computed the heat capacity of a solid. His method is now called the Debye model.
See also
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 27", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 998, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_998.htm.
External links
- Fortran 77 code by Allan MacLeod from Transactions on Mathematical Software
- Fortran 90 version
- "Debye function" entry in MathWorld